本博文假设基本的状态表示和动作表示都已经了解的情况下，对多个强化学习方法进行简要对比

参考文献包括Lilian Wang的A (Long) Peek into Reinforcement Learning，以及笔者就读的CentraleSupelec的课程PPT

Policy definition

策略即给定状态寻找一个动作

DP methods

Dynamic Programming: 对于环境，不同状态不同动作得到的回报我们是完全知道的。

策略分为两步:

  • Policy evalutation: Estimate
  • Policy improvement: Generate

GPI的算法可以写为

For step in [K1, K2, K3...]
    Policy Evaluation:
    Stop when V_(t+1)(s) = V_(t)(s)
Policy improvement

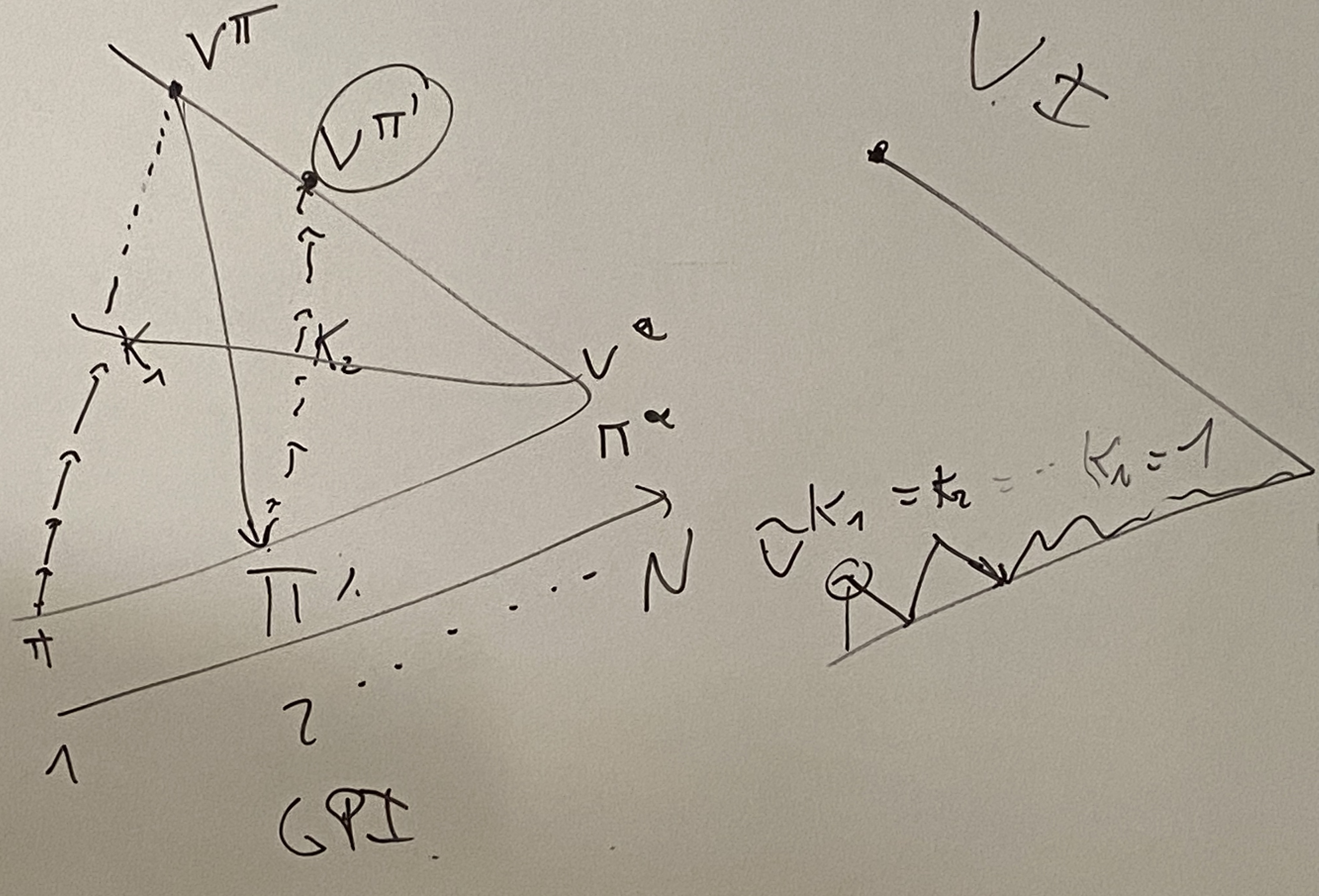
policy_iteration
如图，左边为策略迭代，做K步或者收敛（即到达真实策略时）停止，并进行策略优化。

右图为值迭代，每一步都进行策略的优化。与之相似的为Salsa和Q-Learnings

Sample backups Methods

传统的DP解法：full-width backups
新方法：sample backups， 使用样本的平均值而不是模型预期回报
优势： model free, break curse of dimensionality

Monte-Carlo

使用采样出来的轨迹模拟上述公式

Temporal-Difference Learning:

估计量改为 ，即可得到

比较三种方法

方法 boostrap biase variance backup
DP no — — full, shallow
MC yes no huge with sample, deep
TD yes yes small with sample, shallow

On/Off-policy

Salsa和Q-learning的方法皆为TD Learning的拓展：

On-policy

生成的采样路径都是基于最新的策略的

Off-policy

off-policy learning means learning about one policy from experience generated according to a different policy

生成的采样路径并没有基于最新的策略。
而需要学习的采样策略是基于以往的采样策略进行学习（比如使用importance sampling的方法）

Importance sampling 修正

Q-Learning: Off-policy TD control

Off-policy 是指行动策略和评估策略不同，Q-learning的评估策略是贪婪的，公式对比极易看出

$Q\left(S_{t}, A_{t}\right) \leftarrow Q\left(S_{t}, A_{t}\right)+\alpha\left(R_{t+1}+\gamma \max {a \in \mathcal{A}} Q\left(S{t+1}, a\right)-Q\left(S_{t}, A_{t}\right)\right)$

Double Q-learning

为了解决 Q-learning Overestimation的问题

未完待续

SARSA: On-Policy TD control

Salsa 是和policy iteration相似的方法，
使用 -greedy来获得动作a’（行动策略 和 评估策略）

DL-based RL

Table-based drawback: hard to scale

is parametrised function.

DQN

To present

  • Value, Q function
  • Policy
  • Model

s -[w] ->

s,a -[w] ->

Off-policy, using the greedy way to choose the action

Value Function Approximation

Q-learning will converge

problem:

  • Correlations between samples(especially consecutive state)
  • Non-stationary targets

Solution:

  • Exprience Replay(sample historical )
  • Fixed target

Experience Replay is not the only solution for correlation problem

  • online algorithm: eligibility traces
  • planing with learned models: Dyna-Q
  • change the problem setting: parallel environment

Deadly triad?

when combine Experience Replay+Bootstrap+DL, it supposes to diverge, but in practice, it converges. Called soft-divergence.

Problem: cause value estimate to be poor for extended period.

Solution: Multiple target network

Policy Gradients

Comparison

  • Model-based RL: computing policy is hard and expensive

  • Value-based RL: not the true objective, small value error lead to larger policy error

  • Policy-based RL: right object, but could stuck in local optima, knowledge can be specific , not always generalise well

Stochastic policy

Unlike MDP always with an determistic policy. Most problems are not fully observable. We need to add stochastic policies to increase a bit unstable and have a smoother search space.

Contextual Bandits

one step, use score function to make it gredient-able
$$
\nabla_{\boldsymbol{\theta}} \mathbb{E}{\pi{\boldsymbol{\theta}}}[R(S, A)]=\mathbb{E}{\pi{\boldsymbol{\theta}}}\left[R(S, A) \nabla_{\boldsymbol{\theta}} \log \pi(A \mid S)\right]
$$

Policy Gradient Theorem

$$
\nabla_{\boldsymbol{\theta}} J(\boldsymbol{\theta})=\mathbb{E}{\pi{\boldsymbol{\theta}}}\left[\sum_{t=0}^T \gamma^t q_{\pi_{\boldsymbol{\theta}}}\left(S_t, A_t\right) \nabla_{\boldsymbol{\theta}} \log \pi_{\boldsymbol{\theta}}\left(A_t \mid S_t\right) \mid S_0 \sim d_0\right]
$$

where

$$
\begin{aligned}
q_\pi(s, a) & =\mathbb{E}\pi\left[G_t \mid S_t=s, A_t=a\right] \
& =\mathbb{E}\pi\left[R{t+1}+\gamma q_\pi\left(S{t+1}, A_{t+1}\right) \mid S_t=s, A_t=a\right]
\end{aligned}
$$

Drawback

Policy gradient variations

Solution: Kullbeck-Leibler divergence, minimize the KL-divergence of current the learn policy

then maximize

REINFORCE

使用蒙特卡洛的方法获得一系列轨迹，使用来进行梯度更新

Actor-Critic：结合两部分

既更新策略期望，又更新值函数


Asynchronous Advantage

Actor-Critic (A3C)

异步：多线程 优势：使用优势函数进行更新



异步获得梯度，进行加和，同步更新

Many alternation

TRPO: Trust Region Policy Optimization

PPO: Proximal Policy Optimization

DDPG: Deep Deterministic Policy Gradient

  • can only be used for environments with continuous actions paces

A2C: Advantage Actor-Critic

  • uses advantage estimates value proposition instead of bootstrapping

A3C: Asynchronous Advantage Actor-Critic

  • The convergence rate is faster

SAC: Soft Actor-Critic

  • optimizes a stochastic policy in an off-policy way
  • incorporates the clipped double-Q trick
  • uses entropy regularization (how noise and diverse in the policy)